Introduction to Quantum Computing
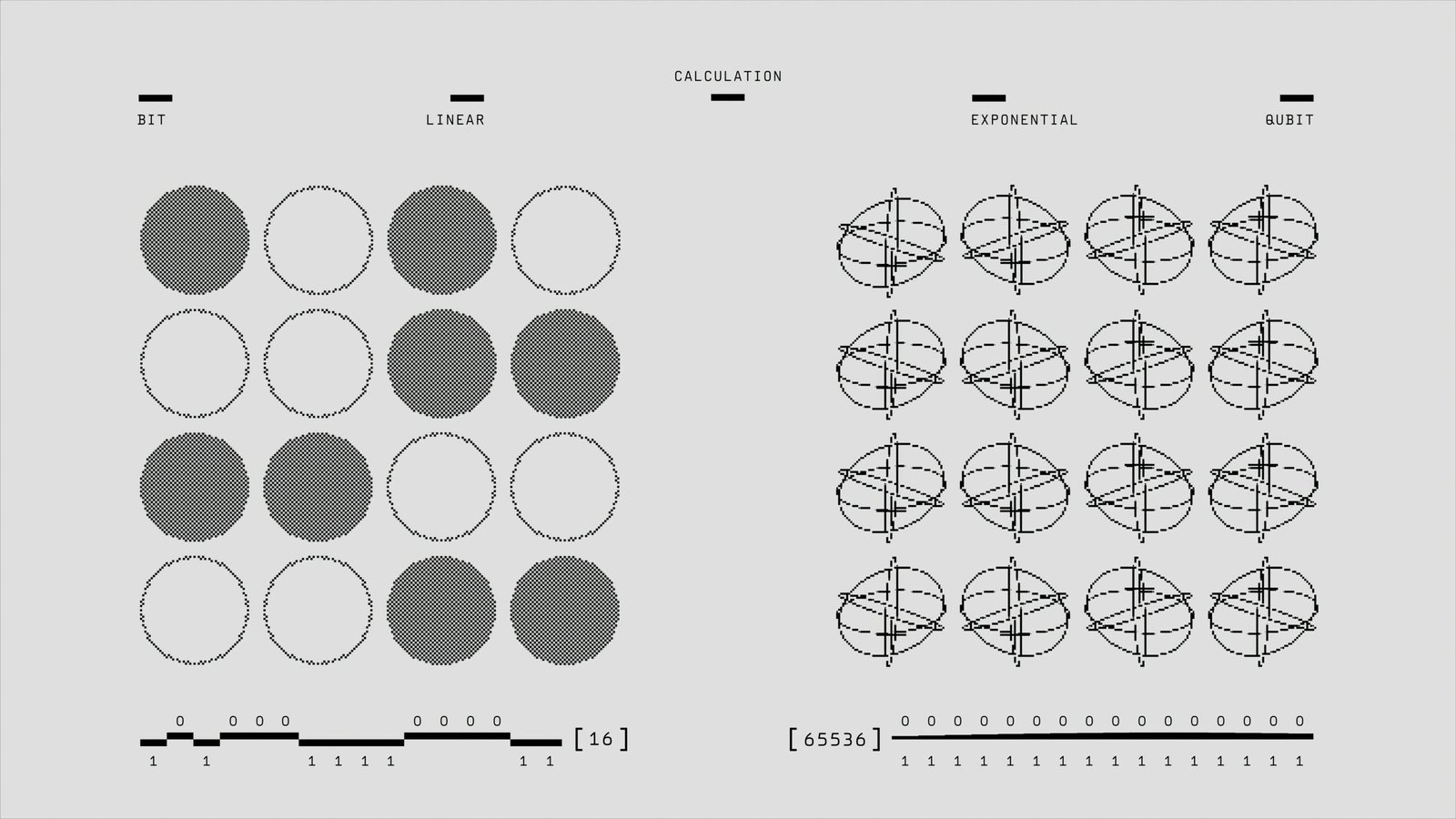
Quantum computing represents a transformative leap in computational technology, diverging significantly from the classical computing paradigm that underpins most of today’s digital infrastructure. At the heart of quantum computing are qubits, which differ fundamentally from classical bits. While a classical bit is binary, existing as either a 0 or a 1, a qubit leverages the principles of quantum mechanics, particularly superposition and entanglement. Superposition allows a qubit to exist simultaneously in multiple states, vastly expanding the computational possibilities.
Entanglement, another cornerstone of quantum mechanics, imbues qubits with an interconnectedness that enables instantaneous state correlation across distances. This phenomenon allows quantum computers to process complex calculations and algorithms at unprecedented speeds. In essence, the simultaneous computation power of qubits exponentially dwarfs that of classical binary bits, posing the potential to solve problems deemed intractable with current technology.
The distinction between classical and quantum computing is not merely incremental but rather a paradigm shift. Classical computers process bits sequentially or in parallel batches, each operation limited to the binary state constraints. In contrast, quantum computers can perform a multitude of computations concurrently, leveraging the probabilistic nature of quantum states.
Recent advancements in quantum computing technology have been marked by significant milestones. Companies like IBM, Google, and Rigetti Computing are at the forefront, developing quantum processors that push the limits of what was previously thought possible. For instance, Google’s announcement of achieving “quantum supremacy” with their Sycamore processor heralded a new era in computational capability, demonstrating the resolution of specific complex problems faster than the most advanced classical supercomputers currently operating.
As quantum technology continues to evolve, it promises not only to accelerate processing speeds but also to revolutionize fields reliant on computational power, such as financial modeling. The potential applications span a multitude of industries, each poised to benefit from the groundbreaking methodologies that quantum computing entails.
Traditional financial modeling methods face several notable challenges that significantly impact their effectiveness. One primary issue is the computational intensity of complex models. For instance, tasks such as option pricing, risk management, and portfolio optimization demand substantial processing power and time. These problems often involve solving multi-dimensional integrals or employing iterative methods that can be exceedingly time-consuming, especially when the models include a large number of variables and constraints.
Another major limitation is the handling and processing of large datasets. Financial markets generate vast amounts of data every second, which must be analyzed swiftly to generate timely insights. Classical computers, constrained by their sequential processing capabilities, often struggle to manage and analyze these massive datasets efficiently. This can lead to delays and bottlenecks, affecting the speed and accuracy of decision-making processes.
Accuracy of predictions is also a significant concern in traditional financial modeling. Financial models are based on various assumptions and approximations, which may not always hold true in real-world scenarios. This inherent uncertainty can lead to significant deviations between predicted and actual outcomes. For example, in option pricing models like Black-Scholes, assumptions about constant volatility and log-normal distribution of asset prices can result in inaccurate pricing, especially in volatile market conditions.
Moreover, risk management models, which are crucial for predicting potential losses and managing financial risk, often rely on historical data to estimate future risks. Such models can be inadequate during periods of market stress or financial crises when past data may not accurately represent future risks, leading to significant underestimations of potential losses.
The limitations of traditional methods become particularly evident when dealing with high-dimensional problems. Portfolio optimization, for example, requires analyzing the expected returns and risks of various asset combinations to identify the optimal portfolio. As the number of assets increases, the complexity and computational requirements grow exponentially, making it impractical for classical computers to find the best solution within a reasonable timeframe.
Potential Applications of Quantum Computing in Finance
Quantum computing holds enormous promise for revolutionizing financial modeling by offering faster and more accurate solutions than classical computing. One of the most compelling applications is in risk assessment. Traditional methods often rely on approximations and simplifications, leading to potential inaccuracies. Quantum computing, however, can process complex datasets and perform intricate calculations exponentially quicker, resulting in more precise risk assessments. For instance, the Quantum Approximate Optimization Algorithm (QAOA) can solve complex optimization problems more efficiently than classical algorithms, making it particularly suited for financial applications.
Another critical area where quantum computing can excel is in the optimization of investment portfolios. Portfolio optimization involves selecting the best mix of investments to achieve a desired return while minimizing risk. Classical algorithms often struggle with the sheer computational load required. Quantum computers, with their ability to handle immense amounts of data simultaneously, can significantly enhance this process. By employing Quantum Monte Carlo simulations, financial analysts can perform more accurate evaluations and simulations, leading to better-informed investment decisions.
Fraud detection algorithms also stand to benefit from quantum computing advancements. Traditional fraud detection relies on pattern recognition and anomaly detection, often limited by computational resources. Quantum algorithms can improve the speed and accuracy of these processes, enabling real-time analysis and faster identification of fraudulent activities. As a result, financial institutions can ensure greater security and reduce the risk of financial losses due to fraud.
Case studies highlight the potential impact of quantum computing in finance. For example, researchers have successfully used quantum algorithms to solve complex optimization problems in milliseconds, which would traditionally take hours or even days. In hypothetical scenarios, a quantum-enhanced risk management system could evaluate market conditions in real-time, providing instantaneous, actionable insights to traders and investors.
In summary, the potential applications of quantum computing in finance are vast and transformative. By utilizing advanced quantum algorithms like QAOA and Quantum Monte Carlo simulations, the financial industry can achieve unprecedented levels of accuracy, speed, and efficiency in various domains such as risk assessment, portfolio optimization, and fraud detection.
Current Developments and Future Prospects
Quantum computing is increasingly being recognized as a game-changer in the field of financial modeling. Recent breakthroughs have set a promising foundation for its integration into financial analytics and risk management. One notable development is the advancement in quantum algorithms, such as the Quantum Approximate Optimization Algorithm (QAOA) and Variational Quantum Eigensolver (VQE), which have shown significant potential in solving complex optimization problems more efficiently than classical computers.
Financial institutions are actively investing in quantum computing research and pilot projects. For instance, multinational banks and financial firms have initiated collaborations with leading technology companies, including IBM and Google, to explore quantum applications. These partnerships aim to leverage quantum capabilities in enhancing portfolio optimization, option pricing, fraud detection, and cryptographic security. Early pilot projects have demonstrated quantum computers’ ability to process vast amounts of financial data at unprecedented speeds, opening new horizons for predictive analytics and market simulation.
However, realizing the full potential of quantum computing in finance comes with challenges. High error rates and the need for error correction present significant hurdles. Current quantum machines also face issues related to qubit stability and coherence time, limiting their practical scalability. Efforts are underway to overcome these barriers, with researchers focusing on developing more robust quantum processors and quantum error correction techniques. Innovations such as superconducting qubits and topological qubits are being explored to enhance stability and reduce error rates.
Looking ahead, the future of quantum computing in financial modeling appears promising. As technological advancements continue, the financial sector stands to undergo profound transformations. Quantum computing could usher in an era of hyper-efficient algorithms, providing unmatched precision in risk assessment and portfolio management. Despite these advancements, widespread adoption will likely span over the next decade, given the current technical and scalability constraints. Financial institutions must remain proactive in their research and development efforts to capitalize on this revolutionary technology as it matures.